Big O וסיבוכיות ריצה
ישנן דרכים רבות לנתח עד כמה טוב הקוד שכתבנו, יש אנשים שמאמינים שקוד יפה יותר טוב ואחרים מעדיפים קוד עם פחות שורות, אך יש דרך אוניברסלית לניתוח אלגוריתם שתעזור לנו להבין כמה יעילה הגישה שלנו.
מה זה Big O Notation ? בקיצור, זוהי הדרך שלנו למדוד את זמן הביצוע ככל שמספר הנתונים גדל (n). מכיוון שהקלט יכול להשתנות Big O ייתן לנו את זמן הריצה המרבי האפשרי מכיוון שלא נוכל להיות בטוחים מראש בתוצאות האפשריות של הפעלת אלגוריתם.
Big O מתאר באופן ספציפי את התרחיש הגרוע ביותר.
זכרו כבר מעכשיו, לרב נשאף להגיע לפתרון שהוא לא מעל (O(N
Constant-Time Algorithm O(1)
(O(1 הוא אלגוריתם שיש לו זמן ריצה קבוע ללא קשר לקלט המסופק (n).
בין אם גודל הקלט שלו הוא אחד או מיליון משך הזמן להשלים את הפעולה ישאר זהה.
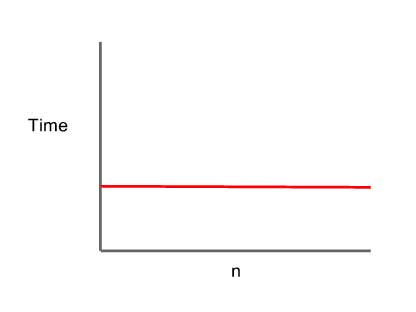
(O(1 הוא התרחיש הטוב ביותר, תמיד כאשר הדבר אפשרי, כדאי לנסות לחפש דרך להשתמש בפונקציות בעלות סימון (O(1
דוגמאות לאלגוריתם שלוקח להם את אותו פרק זמן ולא משנה מה יהיה גודל הקלט: דחיפה למערך, קבלת ערך באינדקס מסוים, הוספת אלמנט ילד וכו..
Linear-Time Algorithm O(N)
(O (n הוא אלגוריתם שיש לו זמן ריצה לינארי לגודל המערך המסופק (n). לולאות הן דוגמה קלאסית לצמיחה לינארית מכיוון שקיים קשר של אחד לאחד בין גודל הנתונים לזמן הריצה. לדוגמא מערך עם 100 פריטים ירוץ פי 5 יותר זמן ממערך של 20 פריטים
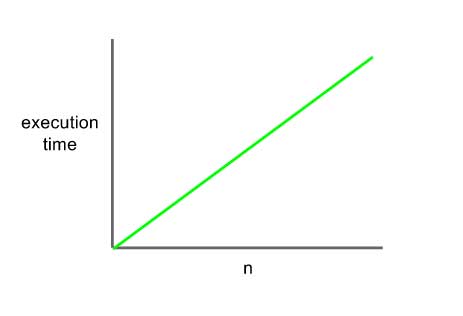
הדוגמא הכי פשוטה להבין (O (n היא פונקציה שמקבלת מערך של מספרים ומדפיסה אותם. אם למערך שלנו יהיו 100 אלמנטים ידרשו 100 איטרציות דרך הלולאה כדי להדפיס את כל הפריטים. אם יהיו לנו מיליון אלמנטים זה ייקח מיליון איטרציות.
אנחנו יכולים לראות בדוגמא שיש מערך אחד שהוא גדול פי 8 מהמערך השני ולכן גם בוצעו עליו פי 8 איטרציות. בואו נראה דוגמא קצת יותר אמיתית כדי שנבין יותר טוב מהו (O (n
תהיו הראשונים לדעת!
הרשמו לניוזלטר שלנו וקבלו התראות על מאמרים חדשים ישירות למייל
(Quadratic-Time Algorithm O(N ^2
(O(N ^2 הוא אלגוריתם שיש לו זמן ריצה ריבועי שבו הביצוע פרופורציונלי לריבוע גודל הקלט (n).
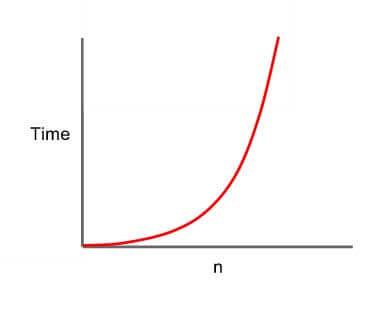
לדוגמא, אלגוריתם של bubble sort המכיל קלט של 5 פריטים פועל 5 פעמים על הלולאה החיצונית והלולאה הפנימית פועלת 5 פעמים להפעלת הלולאה החיצונית, או בקיצור לולאות מקוננות ( n * n).
בחרתי בכוונה בגרסא הכי קריאה ופשוטה להבנה של bubble sort. כמובן שאפשר לבצע לזה אופטימיזציה (לחצו לדוגמא) אבל עדיין נשאר עם (O(N ^2.
לאגלוריתם זה יש אפשרות לרוץ ב- (O (n והיא אם קיבלנו כבר מערך ממויין מראש! אבל מכיוון שב- Big O שאנחנו הולכים על ה-worst-case אלגוריתם זה ישאר ברמת סיבוכיות (O(N ^2.
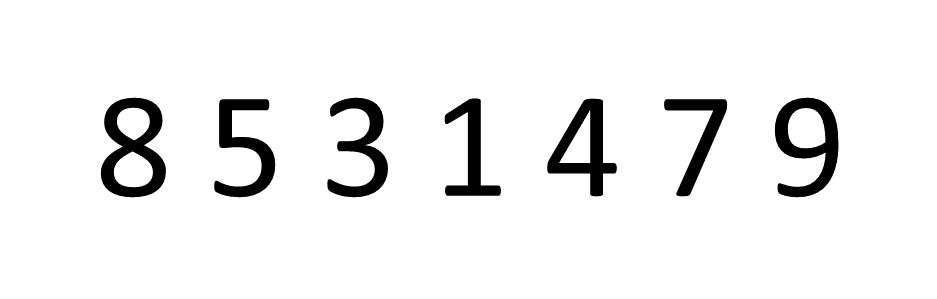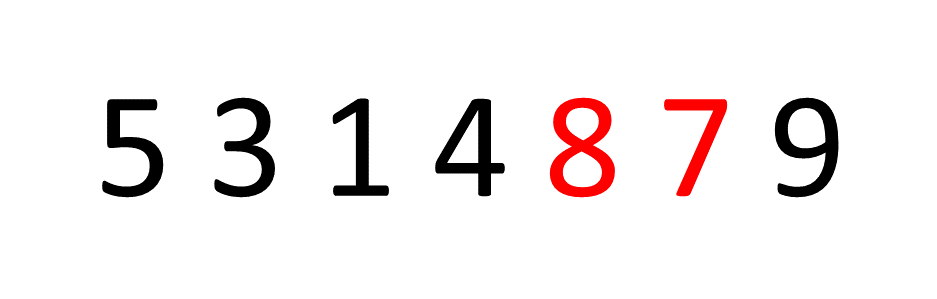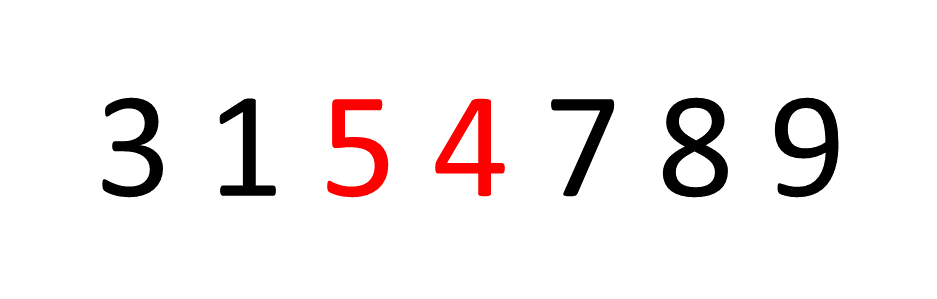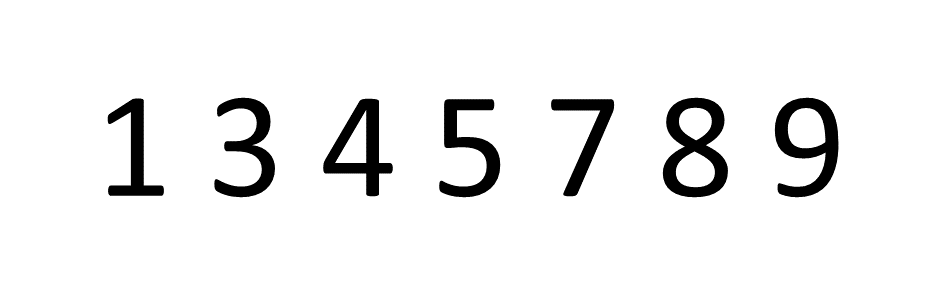
(Logarithmic time O(log n
האנלוגיה הטובה ביותר ששמעתי להבין מהי צמיחה לוגריתמית היא לדמיין חיפוש של מילה כמו במילון. לצורך הדוגמא נחפש את המילה ״ריאקט״. אנחנו לא נחפש ערך ערך, במקום זאת נפתח את המילון באמצע נראה באיזה אות פתחנו למשל באות ״כ״ נדע שכל מה שלפני ״כ״ כבר לא רלוונטי לנו ונמשיך הלאה, עשינו עוד דפדוף והגענו לאות ״ע״ ושוב נדע שכל מה שלפני הדף שפתחנו גם לא רלוונטי וכך בעצם נמשיך עד שנגיע לערך שחיפשנו.
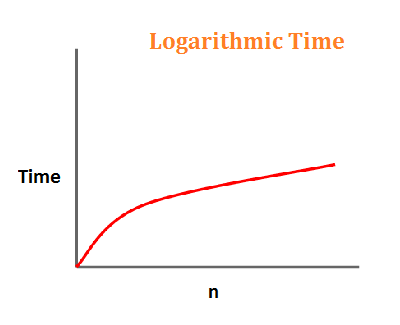
משך הזמן למצוא משהו עדיין ישתנה בהתאם לגודל המילון, אך בשום מקום לא קרוב לקצב של (O (n מכיוון ש-(O(log n מחפשת במקטעים ספציפיים יותר בהדרגה מבלי להסתכל על מרבית הנתונים.
(O(log n הוא האלגוריתם היעיל ביותר כאשר מערך הנתונים (n) המסופק גדול. חיפוש באלף פריטים עשוי להימשך פחות מ -10 פעולות ואילו מיליון עשויים להימשך פחות מ -20 פעולות.
דוגמה קלאסית לאלגוריתם (O(log n תהיה אלגוריתם חיפוש בינארי.
מקווה שהקוד קריא וברור(העניין הוא חלוקה למקטעים). מי שלא הצליח לעקוב אני בטוח שהגיף הבא יעזור לכם.

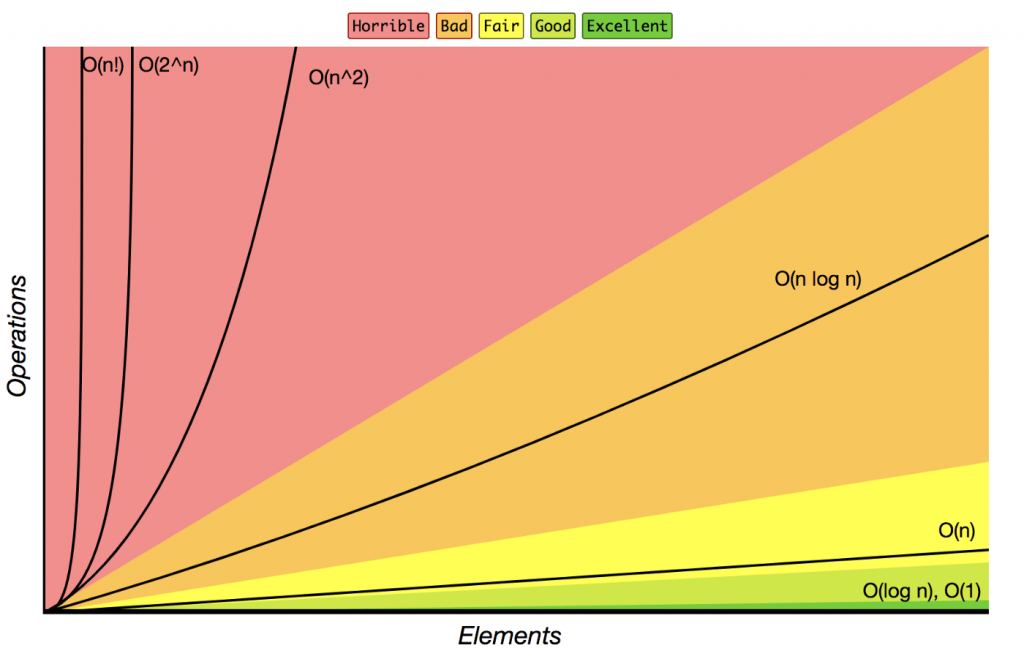
סקרנו את הרמות סיבוכיות הנפוצות אך שימו לב שיש עוד סוגים שלא עברנו עליהם. הגרף הבא יעזור לנו להבין את רמות הסיבוכיות וכמה הן יעילות. שימו לב ש- (O(N ^2
כבר בקטגוריה האדומה :/
חישוב סיבוכיות ריצה
ניקח אלגוריתם שמריץ שלוש פעולות
- (constant operation O(1
2. (A Linear operation O(n
3. (A Quadratic operation O(n²
נוכל לחשוב שצריך לסכם את הכל בצורה הזו (O (1) + O (n) + O (n², נכון?
אז לא, זה הרבה יותר פשוט. אנחנו נתעלם מהפעולות המהירות יותר וניקח בחשבון רק את הפעולה האיטית ביותר, במקרה זה, (O (n², אז זהו אלגוריתם עם סימון (O (n².
אבל מה היה קורה אם היה לנו אלגוריתם שיש בו פעמיים (O (n² ? האם רמת הסיבוכיות שלו הייתה (O (2n². אז גם פה זה פשוט יותר. אנחנו מתעלמים מקבועים וגם אלגוריתם זה יהיה (O (n²
כמובן שיש המון אלגוריתמים שזמני הריצה שלהם ידועים לנו אז קבלו אתר מעולה שמרכז המון מהם – https://www.bigocheatsheet.com
בואו נראה דוגמא איך אנחנו יכולים לייעל אלגוריתם.
הפונקציה הבאה תרוץ ב- (O (n, ככל שגודל המערך יגדל הלולאה תרוץ n פעמים
לא צריך להיות אלגוריתמיקאי מחונן כל הקטע בתכנות זה פתירת בעיות וככל שנכיר יותר מקרים ונצבור יותר ידע יהיה לנו קל יותר.
כדי לסכום מערך מגודל 1..n אנחנו יכולים להשתמש בנוסחא הבאה וכעת הפונקציה שלנו תרוץ ב- (O(1 מכיוון שללא קשר לגודל הקלט, האלגוריתם שלנו יבצע את אותו הפעולה.
const res = (n * (n+1)) / 2;n- מייצג את גודל המערך
לסיכום
כמפתחים תמיד נרצה שהקוד שלנו יהיה יעיל (וקריא) ככל הניתן ו- Big O Notation הוא כלי חשוב לכל מפתח על מנת לגרום לקוד שלו להיות כזה.
אשמח אם תשתפו/תמליצו לאחרים, אם יש לכם שאלות או הערות תוכלו להשאיר אותם בתגובות מתחת או ליצור איתי קשר בלינקדין.
ישנן דרכים רבות לנתח עד כמה טוב הקוד שכתבנו, יש אנשים שמאמינים שקוד יפה יותר טוב ואחרים מעדיפים קוד עם פחות שורות, אך יש דרך אוניברסלית לניתוח אלגוריתם שתעזור לנו להבין כמה יעילה הגישה שלנו.
מה זה Big O Notation ? בקיצור, זוהי הדרך שלנו למדוד את זמן הביצוע ככל שמספר הנתונים גדל (n). מכיוון שהקלט יכול להשתנות Big O ייתן לנו את זמן הריצה המרבי האפשרי מכיוון שלא נוכל להיות בטוחים מראש בתוצאות האפשריות של הפעלת אלגוריתם.
Big O מתאר באופן ספציפי את התרחיש הגרוע ביותר.
זכרו כבר מעכשיו, לרב נשאף להגיע לפתרון שהוא לא מעל (O(N
Constant-Time Algorithm O(1)
(O(1 הוא אלגוריתם שיש לו זמן ריצה קבוע ללא קשר לקלט המסופק (n).
בין אם גודל הקלט שלו הוא אחד או מיליון משך הזמן להשלים את הפעולה ישאר זהה.

(O(1 הוא התרחיש הטוב ביותר, תמיד כאשר הדבר אפשרי, כדאי לנסות לחפש דרך להשתמש בפונקציות בעלות סימון (O(1
דוגמאות לאלגוריתם שלוקח להם את אותו פרק זמן ולא משנה מה יהיה גודל הקלט: דחיפה למערך, קבלת ערך באינדקס מסוים, הוספת אלמנט ילד וכו..
Linear-Time Algorithm O(N)
(O (n הוא אלגוריתם שיש לו זמן ריצה לינארי לגודל המערך המסופק (n). לולאות הן דוגמה קלאסית לצמיחה לינארית מכיוון שקיים קשר של אחד לאחד בין גודל הנתונים לזמן הריצה. לדוגמא מערך עם 100 פריטים ירוץ פי 5 יותר זמן ממערך של 20 פריטים

הדוגמא הכי פשוטה להבין (O (n היא פונקציה שמקבלת מערך של מספרים ומדפיסה אותם. אם למערך שלנו יהיו 100 אלמנטים ידרשו 100 איטרציות דרך הלולאה כדי להדפיס את כל הפריטים. אם יהיו לנו מיליון אלמנטים זה ייקח מיליון איטרציות.
אנחנו יכולים לראות בדוגמא שיש מערך אחד שהוא גדול פי 8 מהמערך השני ולכן גם בוצעו עליו פי 8 איטרציות. בואו נראה דוגמא קצת יותר אמיתית כדי שנבין יותר טוב מהו (O (n
תהיו הראשונים לדעת!
הרשמו לניוזלטר שלנו וקבלו התראות על מאמרים חדשים ישירות למייל
(Quadratic-Time Algorithm O(N ^2
(O(N ^2 הוא אלגוריתם שיש לו זמן ריצה ריבועי שבו הביצוע פרופורציונלי לריבוע גודל הקלט (n).

לדוגמא, אלגוריתם של bubble sort המכיל קלט של 5 פריטים פועל 5 פעמים על הלולאה החיצונית והלולאה הפנימית פועלת 5 פעמים להפעלת הלולאה החיצונית, או בקיצור לולאות מקוננות ( n * n).
בחרתי בכוונה בגרסא הכי קריאה ופשוטה להבנה של bubble sort. כמובן שאפשר לבצע לזה אופטימיזציה (לחצו לדוגמא) אבל עדיין נשאר עם (O(N ^2.
לאגלוריתם זה יש אפשרות לרוץ ב- (O (n והיא אם קיבלנו כבר מערך ממויין מראש! אבל מכיוון שב- Big O שאנחנו הולכים על ה-worst-case אלגוריתם זה ישאר ברמת סיבוכיות (O(N ^2.
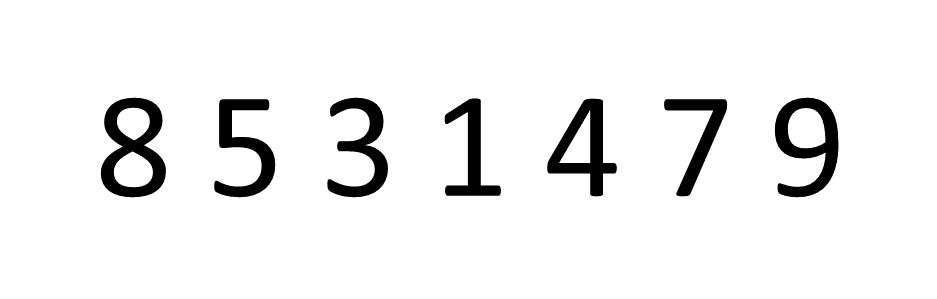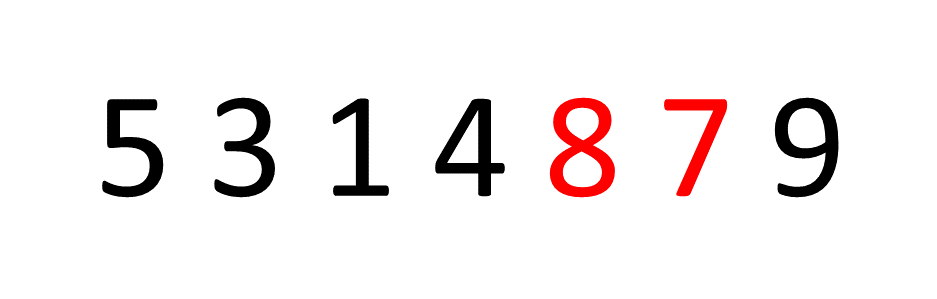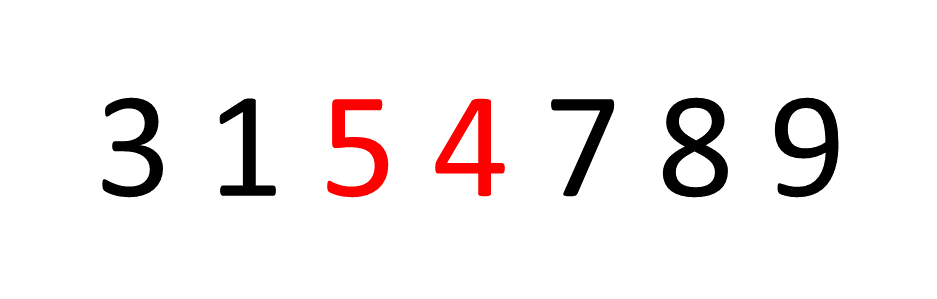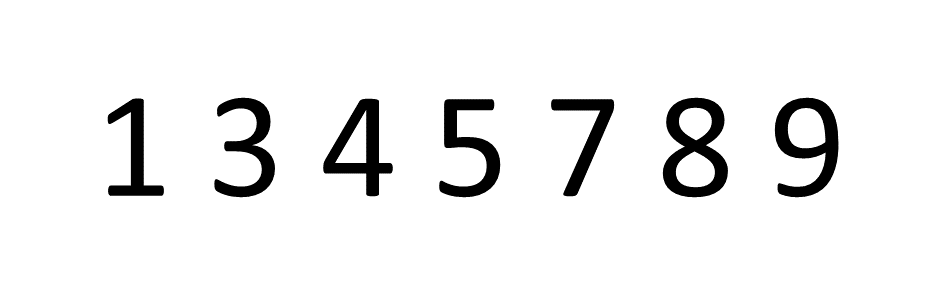
(Logarithmic time O(log n
האנלוגיה הטובה ביותר ששמעתי להבין מהי צמיחה לוגריתמית היא לדמיין חיפוש של מילה כמו במילון. לצורך הדוגמא נחפש את המילה ״ריאקט״. אנחנו לא נחפש ערך ערך, במקום זאת נפתח את המילון באמצע נראה באיזה אות פתחנו למשל באות ״כ״ נדע שכל מה שלפני ״כ״ כבר לא רלוונטי לנו ונמשיך הלאה, עשינו עוד דפדוף והגענו לאות ״ע״ ושוב נדע שכל מה שלפני הדף שפתחנו גם לא רלוונטי וכך בעצם נמשיך עד שנגיע לערך שחיפשנו.

משך הזמן למצוא משהו עדיין ישתנה בהתאם לגודל המילון, אך בשום מקום לא קרוב לקצב של (O (n מכיוון ש-(O(log n מחפשת במקטעים ספציפיים יותר בהדרגה מבלי להסתכל על מרבית הנתונים.
(O(log n הוא האלגוריתם היעיל ביותר כאשר מערך הנתונים (n) המסופק גדול. חיפוש באלף פריטים עשוי להימשך פחות מ -10 פעולות ואילו מיליון עשויים להימשך פחות מ -20 פעולות.
דוגמה קלאסית לאלגוריתם (O(log n תהיה אלגוריתם חיפוש בינארי.
מקווה שהקוד קריא וברור(העניין הוא חלוקה למקטעים). מי שלא הצליח לעקוב אני בטוח שהגיף הבא יעזור לכם.

סקרנו את הרמות סיבוכיות הנפוצות אך שימו לב שיש עוד סוגים שלא עברנו עליהם. הגרף הבא יעזור לנו להבין את רמות הסיבוכיות וכמה הן יעילות. שימו לב ש- (O(N ^2
כבר בקטגוריה האדומה :/

חישוב סיבוכיות ריצה
ניקח אלגוריתם שמריץ שלוש פעולות
- (constant operation O(1
2. (A Linear operation O(n
3. (A Quadratic operation O(n²
נוכל לחשוב שצריך לסכם את הכל בצורה הזו (O (1) + O (n) + O (n², נכון?
אז לא, זה הרבה יותר פשוט. אנחנו נתעלם מהפעולות המהירות יותר וניקח בחשבון רק את הפעולה האיטית ביותר, במקרה זה, (O (n², אז זהו אלגוריתם עם סימון (O (n².
אבל מה היה קורה אם היה לנו אלגוריתם שיש בו פעמיים (O (n² ? האם רמת הסיבוכיות שלו הייתה (O (2n². אז גם פה זה פשוט יותר. אנחנו מתעלמים מקבועים וגם אלגוריתם זה יהיה (O (n²
כמובן שיש המון אלגוריתמים שזמני הריצה שלהם ידועים לנו אז קבלו אתר מעולה שמרכז המון מהם – https://www.bigocheatsheet.com
בואו נראה דוגמא איך אנחנו יכולים לייעל אלגוריתם.
הפונקציה הבאה תרוץ ב- (O (n, ככל שגודל המערך יגדל הלולאה תרוץ n פעמים
לא צריך להיות אלגוריתמיקאי מחונן כל הקטע בתכנות זה פתירת בעיות וככל שנכיר יותר מקרים ונצבור יותר ידע יהיה לנו קל יותר.
כדי לסכום מערך מגודל 1..n אנחנו יכולים להשתמש בנוסחא הבאה וכעת הפונקציה שלנו תרוץ ב- (O(1 מכיוון שללא קשר לגודל הקלט, האלגוריתם שלנו יבצע את אותו הפעולה.
const res = (n * (n+1)) / 2;n- מייצג את גודל המערך
לסיכום
כמפתחים תמיד נרצה שהקוד שלנו יהיה יעיל (וקריא) ככל הניתן ו- Big O Notation הוא כלי חשוב לכל מפתח על מנת לגרום לקוד שלו להיות כזה.
אשמח אם תשתפו/תמליצו לאחרים, אם יש לכם שאלות או הערות תוכלו להשאיר אותם בתגובות מתחת או ליצור איתי קשר בלינקדין.

10 תגובות
מאמר מעולה! ממש מוסבר ברור. רק הערה קטנה לגבי חיפוש בינארי והסיבוכיות, צריך להדגיש שהסיבוכיות הזו יוצאת מתוך ההנחה שהמערך ממומיין מראש. למרות שלפי מה שכתבת זה לא מחושב ככה אלא רק על ידי ערך הסיבוכיות הגבוה ביותר.
היי מיה
אכן חיפוש בינארי יעבוד רק על מערכים ממויינים.
ללא קשר תמיד שנבדוק סיבוכיות של אלגוריתם מסויים ב Big O נלך על ה worst-case.
אולי לא הבנתי איפה את רואה את הסתירה פה?
מסכימה
היי רועי גם אני חושב שהמאמר מוסבר בצורה ממש טובה וזה כבר השני שאני קורא אצלך ושאפו גדול על האתר.
בנוסף, הצירוף של הגיפים ממש קול.
1. אני גם חושב כמו מיה שראוי לציין בעבור אלו שלא מכירים חיפוש בינארי שהחיפוש יעבוד רק על מערכים שמסודרים מהנמוך לגבוה (או הפוך אם מסדרים קצת את האלגוריתם)
2. לגבי הפונקציית סכימה גם צריך לציין שהנוסחה תעבוד על מערכים עם ערכים שרצים מ 1..n *בצעדים של 1* כי אם למשל הערכים יקפצו בצעדים של 3 או שפשוט יהיו רנדומילם האלגוריתם לא היה נכון.
תודה רבה ותמשיך להעלות תוכן מעולה =]
אתה בטוח לגבי המערך? O(1)?
היי , לא ראיתי מקום שמסביר טוב כמו פה . ולכן אשמח אם תרחיב על
2^n
n^n
n^n!
תודה רבה. אנסה למצוא זמן ולהרחיב את הבלוג פוסט
מאמר מעולה! מוסבר נהדר !
מאמר מצויין
מאמר מצוין תודה רבה
מוסבר בהיר וברור
גם אני אשמח מאד אם תעלה הסברים ברורים כאלו גם על
2^n
n^n
n^n!